Unit 2: Portfolio

Portfolio Theory

Concept of Risk

In finance, risk refers to the possibility of losing money or not getting expected returns from an investment. It's the uncertainty associated with future returns.

• Return = Reward
• Risk = Uncertainty or chance of loss

Components of Risk

Risk is mainly divided into two components:

Component	Meaning	Example
Systematic Risk	Market-related risk; cannot be diversified	Inflation, interest rates, recession
Unsystematic Risk	Company-specific or industry-specific risk; can be diversified	Poor management, labor strike

Measurement of Risk

The most common measures of risk in finance:

Risk Measure	Description
Standard Deviation (σ)	Measures how much the return deviates from the average. Higher σ = higher risk.
Variance (σ²)	Square of standard deviation. Used to calculate portfolio risk.
Beta (β)	Measures how much a security moves relative to the market. Beta > 1 means more volatile than market.

Covariance

• Covariance measures how two securities move together.
• If positive, they tend to move in the same direction.
• If negative, they move in opposite directions.

Correlation (ρ)

• Correlation coefficient is a standardized form of covariance.
• It ranges from -1 to +1.

Value of ρ	Interpretation
+1	Perfect positive correlation
0	No correlation
-1	Perfect negative correlation

Fundamental Coefficient (Beta - β)

• Beta is a key coefficient in portfolio theory.
• Measures the systematic risk of a security compared to the market.

Beta (β)	Meaning
= 1	Same risk as the market
> 1	More volatile than the market
< 1	Less volatile than the market

Where:

• $R_i$: Return on asset

• $R_m$: Return on market

• $\sigma^2_m$: Variance of market return

Summary Table

Measurement of Systematic Analysis

Systematic analysis helps investors assess market-wide risks that impact all investments, not just a specific company. It includes top-down analysis across 3 levels:

Economic Analysis

Economic analysis studies macroeconomic factors affecting the overall financial market.

Industry Analysis

It examines the health, growth, and competition of a particular industry.

Key Factors

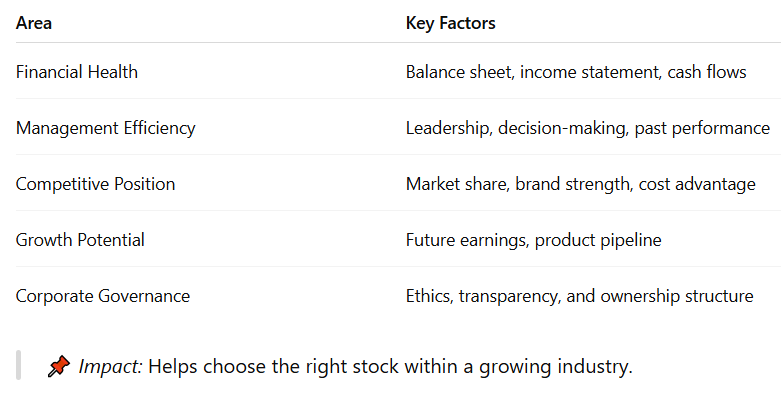
Company Analysis

This focuses on individual firm performance.

Key Areas

Portfolio Risk and Return

Return of a Portfolio

Weighted average of returns of all assets in the portfolio.

Where:

• $R_p$: Portfolio return

• $w_i$: Weight of asset $i$ in portfolio

• $R_i$: Return of asset $i$
  

Portfolio Risk (Standard Deviation)

For a 2-asset portfolio:

Where:

• $w_1, w_2$: weights of assets

• ${\sigma }_1,:\; standard\; deviations$

• $\rho_{12}$: correlation between assets

Diversification helps reduce unsystematic risk, but systematic risk (market risk) always remains.

Beta as a Measure of Systematic Risk

Beta (β) measures how much a stock or portfolio reacts to market movements.

Interpretation

 Formula

Where:

• $R_i$: Return of the asset

• $R_m$: Return of the market

• $\sigma^2_m$: Variance of market return

📌 Use of Beta: Helps in Capital Asset Pricing Model (CAPM) to find expected return:

Calculation of Beta (β)

Beta measures a stock’s sensitivity to market movements. It shows how much a security’s returns change in relation to market returns.

Formula:

Where:

• $R_i$: Return of the individual asset

• $R_m$: Return of the market

• Cov: Covariance between asset and market

• Var: Variance of the market

Alternative (Regression-Based) Formula:

Using statistical tools or Excel, you can run a regression:

Beta Value	Meaning
β = 1	Moves exactly like the market
β > 1	More volatile than the market (aggressive)
β < 1	Less volatile (defensive)
β = 0	No market sensitivity
β < 0	Moves opposite to market

Selection of Portfolio

Portfolio selection involves choosing the best combination of assets to maximize returns and minimize risk.

• A. Markowitz’s Modern Portfolio Theory (MPT)
• Proposed by Harry Markowitz in 1952
• Focuses on diversification to reduce unsystematic risk

Key Concepts:

• Investors are risk-averse
• Portfolio return is weighted average of individual returns
• Portfolio risk depends on variance and correlation

Efficient Frontier

• A graph showing optimal portfolios that offer the highest return for a given level of risk.
• Portfolios below the frontier are sub-optimal.
• The tangent to the frontier from the risk-free rate gives the optimal risky portfolio.

Portfolio Return:

 Portfolio Risk (2 assets)

Goal: Minimize σp for a given Rp → choose assets with low or negative correlation

• B. Single Index Model (Sharpe’s Model)
• Proposed by William Sharpe
• Simplifies Markowitz model by assuming that stock returns are influenced only by the market index (like Nifty/Sensex)

Formula

Advantages Over MPT